A review on global wind power forecasting approaches

Wind energy has become one of the most widely preferred energy sources over the last decades given its sustainable and environmentally friendly nature. Many countries are now promoting and supporting their local wind energy industry. For example, the US plans to increase the total electricity provided by wind power up to 20% by 2030 (Lindenberg, Smith, &O’Dell, 2008). However, since the amount of wind energy generated in wind turbine directly depends on wind speed, which has time-varying nature and depends on topological features of location, it is a challenging task for the electricity market members to keep balance between power demand and power supply to avoid the financial and technical losses. Therefore in order to use the wind energy in a full potential, it is essential to find an effective wind power forecasting method that considers all the nuances of wind nature properly. 

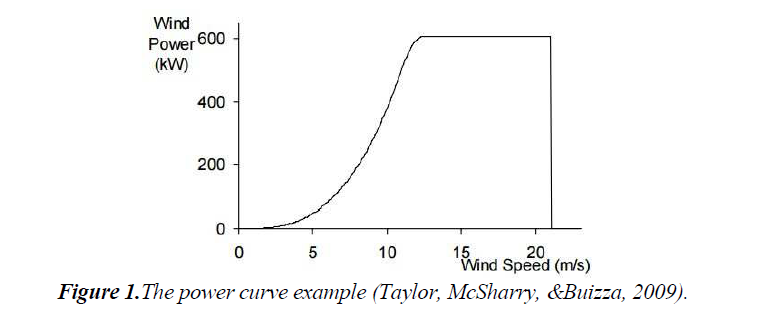
Wind energy has become one of the most widely preferred energy sources over the last decades given its sustainable and environmentally friendly nature. Many countries are now promoting and supporting their local wind energy industry. For example, the US plans to increase the total electricity provided by wind power up to 20% by 2030 (Lindenberg, Smith, &O’Dell, 2008). However, since the amount of wind energy generated in wind turbine directly depends on wind speed, which has time-varying nature and depends on topological features of location, it is a challenging task for the electricity market members to keep balance between power demand and power supply to avoid the financial and technical losses.It is clear that there is a nonlinear relationship between wind power and wind speed. Due to their cubic relationship, the small error in forecasted wind speed can lead to large error in wind power forecast. In Figure 1, the power curve plot shows that relationship between wind power and wind speed as well as the existence of “disconnection speed”, when in practice the turbine controls the generation of wind power during extremely strong wind (Taylor, McSharry, &Buizza, 2009).Therefore in order to use the wind energy in a full potential, it is essential to find an effective wind power forecasting method that considers all the nuances of wind nature properly.

Figure 1.The power curve example (Taylor, McSharry, &Buizza, 2009).

According to Soman and Zareipour (2010), the wind power forecasting time periods can be classified into the following levels: 1) Very short-term (few seconds to 30 minutes ahead), 2) Short-term (30 minutes to 6 hours ahead), 3) Medium-term (6 hours to 1 day ahead) and 4) Long-term (1 day to 1 week or more ahead). As numerous literatures including Jung and Broadwater (2014) state, most common wind forecasting methods can be divided into three major groups: physical, statistical and hybrid approaches. The objective of the article is to reviewthe existing wind power forecasting techniques that are based on numeric weather prediction (NWP), time series and artificial neural network methods (ANN) and their combinations that give the most accurate forecast results in different time scales.

Numeric Weather Prediction (NWP) method is a physical approach that isused for forecasting wind power. It solves complex mathematical models using regional meteorological data including physical features like wind speed and its direction, temperature, air pressure and NWP models usually give the most accurate results for long term (more than 1 day) predictions compared to other methods, but it is computationally expensive (Li et al., 2001).

One of the NWP based methods is called High-resolution limited area model (HIRLAM), which was developed by the Scandinavian Meteorological Institutes (Machenhauer, 1988). In order to forecast the wind power, the forecasted wind speedby HIRLAM is changed to the surface with the geostrophic drag law. For further details one can refer to Landberg (1994). In order to get local wind prediction it is essential to consider the local effects, which was done with WASP (Wind Atlas Analysis and Application Program). After obtaining predicted wind power using the power curve, Model Output Statistics (MOS) is applied to scale the output of the model from and correct it from bias. Landberg (1999) applied the model for one year data set of 10 Danish wind farms between February 1995 and January 1996, which contains the regional physical features for every 10 minutes. The model is used for all the wind farms to predict wind power up to 36 hours ahead, the computation of which took 4 hours. For the assessment purpose of the results forecasted with HIRLAM, the persistence model was also built on that data. According to the Mean Square Errors (MAE) of two models, HIRLAM beats the persistence model for the long term prediction period (more than 4 hours ahead). Besides HIRLAM, there exist other numerous NWP models like Global Forecasting Systems, MM5, Prediktor, but their output forecasts are not as accurate as they give in combination with other methods (Soman&Zareipour, 2010).

Statistical methods need historical data to build statistical models to forecast wind power and provide cheaper and easier ways of implementation compared to the physical According to Chan (2013), the main drawback of statistical models is that the prediction error grows as prediction time horizon increases. Therefore, statistical methods are the most effective for very short-term and short-term (less than 6 hours ahead) wind power predictions.

The most popular statistical method for wind power prediction is Persistence Method. It assumes that wind speed or wind power P(t+h) at time point ‘t+h’ will be the same as it was at time point ‘t’: P(t+h)=P(t) (Landberg, 1999). Surprisingly, this method is very accurate for very short term and short term (less than 6 hours ahead) predictions (Soman&Zareipour, 2010). Due its simplicity, it is usually used as a benchmark for wind power prediction models.

Auto-Regressive Moving Average (ARMA) models are well-known time series based techniques.One can see from the equation of ARMA (p, q), where X at time t is a linear combination of past observations of X starting from time ‘t-p’ and white noise series with order q and with zero mean and variance sigma (Milligan, Schwartz & Wan, 2003). In the literature of wind power forecasting methods, different types of ARMA models are reported including Auto-Regressive Integrated Moving Average (ARIMA), seasonal-ARIMA, fractional-ARIMA, and ARMA models with exogenous variables (ARMAX or ARX).

Milligan, Schwartz, and Wan (2003) investigated the performance of differentARMA based models in wind power forecast and applied the models for historical data generated in wind power plants of Iowa and Minnesota, US. Initially, ARMA models with specified orders were trained for the data set of January, 2001 of both wind plants and were tested the forecasting models for February. The root means squared errors (RMSE) of the forecasted results up to 6 hours ahead are compared with the RMSE that obtained by the persistence method. Comparing their RMSEs of different ARMA models with the persistence model, ARMA (1,24) gave the most accurate results over the persistence model, by 7% better for 1 hour ahead and about 18% for 6 hours ahead prediction.

Neural network (NN) based approaches are also one of the widely used types of statistical methods that predict wind power by using long historical data and learning the relationship between input and output variables. It demonstrates the multi-layer neural network scheme, where Xiis ithinput variable and Yiis the output. Where Xjis the jthinput, Yi is the output, Wij is the weight connecting node i to node j, bi is the bias of the node, and fi is an activation function (Tesfaye et al., 2016).

Tesfayeet al. (2016) presented feed forward ANN with back propagation learning algorithm that predicts wind power based on learning the relationship between wind speed and wind power. The model forecasts 1 day ahead wind power for every 10 minutes using one year data set of wind speed and wind power between 26th March 2014 and 25th March 25 2016 (on 10 minutes interval basis). The data is obtained from Goldwindmicrogrid wind turbine system, Beijing, China. To train the feed forward ANN model for the dataset, the wind speed and wind powerare used as training (input) and target (output) variables respectively. After being trained on the dataset from Goldwind, feed forward ANN model utilizes the forecasted 4 days wind speed data (26 th March 2015 to the 29th March 2015) obtained from Numeric Weather Prediction system to get wind power output values for one day ahead with 10 minutes interval (144 wind power values). The predicted wind power of the NN model was compared to the actual wind power values and the accuracy of the method was quite high with mean absolute errors around 12-15% for each day.

The third major group of wind power forecasting methods is called hybrid approaches, which combines different forecastingapproaches to enhance the prediction accuracy. For example, Potter and Negnevitsky (2006) analyze the combination of adaptive neural network and fuzzy logic in their paper. They applied an adaptive neuro-fuzzy inference system (ANFIS) proposed by Roger Jang (1993) for the prediction of wind vectors for every 2.5 minutes ahead in Tasmania, The paper aimed to predict wind vectors, since wind direction is very important to maximize the generation of wind power in very short-time (2.5 minutes). An ANFIS model consists of six layer feedforward neural network: 1) input layer, 2) fuzzification layer, 3) rule layer, 4) normalization layer, 5) defuzzification layer, and 6) ANFIS output – y.

x1 and x2 are assumed to be two input variables and y is the output. There are two fuzzy sets for each input: A1 and A2 are fuzzy sets on the universe of discourse X1; B1 and B2 are fuzzy sets on the universe of discourse X2; Layer 1 is the input layer. In each layer ANFIS model uses the algorithms of the least square estimator and the gradient descent method to compute the networkweights and obtain the output forecast. When the model was used for 21 months time series dataset of wind sites in Tasmania, mean absolute squared errors (MAPE) of an ANFIS model was much smaller than the MAPE of the persistence method (4% versus 30% respectively).

In this paper, a review on different wind power forecast approaches were presented. A brief description was provided for each method and several forecasting models were discussed. Analyzing the performances of physical, statistical and hybrid models, strong and weak sides of each method were demonstrated.

References

1. Chang Y. (2014). A Literature Review of Wind Forecasting Methods. Journal of Power and Energy Engineering, 2, 161-168.
2. Jang J.-S. (1993). ANFIS: adaptive network-based fuzzy inference systems. IEEE Trans. Syst., Man, Cybern. 23(3), pp. 665–685.
3. Jung J., and R. (2014).Current status and future advances for wind speed and power forecasting.Renewable and Sustainable Energy Review. 31, 762-777.
4. Landberg (1999). Short-term prediction of the power production from wind farms. Journal of Wind Engineering and Industrial Aerodynamics. 80:207-20.
5. Li S., Wunsch, D.C., O’Hair, , and Gieselman, M.G. (2001). Using neural networks to estimate wind turbine power generation." IEEE Transactions on energy conversion. 16(3), pp. 276-282.
6. Lindenberg , Smith, B., and O’Dell, K. (2008). 20% wind energy by 2030. National renewable energy laboratory (NREL), US department of energy, renewable energy consulting services, energetics incorporated .
7. Landberg and Watson, S.J. (1994). Short-term prediction of local wind conditions, Bound-Layer Meteorol. 70, 1 71-195.
8. Machenhauer (Ed.), (1988). HIRLAM final report, HIRLAM Technical Report 5, Danish Meteorological Institute, Copenhagen, Denmark.
9. Milligan, M., Schwartz, M., and Wan, (2003). Statistical wind power forecasting models: Results for U.S. wind farms. in Proc. Windpower, Austin, TX, May 18–21, NREL/CP-500-33 956
10. Potter, W. and Negnevitsky, M. (2006). Very short-term wind forecasting for Tasmanian power generation. IEEE Trans. Power Syst. 21(2), pp. 965- 972.
11. Troen, and Petersen, E.L. (1989). The European Wind Atlas, Published for the CEC by Ris+ National Laboratory, Roskilde, Denmark, 656 pp.
12. Soman, S. and Zareipour, H. (2010). A Review of Wind Power and Wind Speed Forecasting Methods With Different Time Horizons, IEEE Trans. Power Syst.
13. Taylor, J.W.,McSharry, P.E., and Buizza, (2009). Wind power density forecasting using ensemble predictions and time series models, IEEE Trans. Energy Convers., 24(3), pp. 775-782
14. Tesfaye, A., Zhang, H., Zheng, D. H. and Shiferaw, D. (2016). Short-Term Wind Power Forecasting Using Artificial Neural Networks for Resource Scheduling in Microgrids. International Journal of Science and Engineering Applications (iJSEA. 5(3).