В статье рассматриваются алгоритмы определения принадлежности точки многоугольнику.
Предлагается способ ускорения поиска многоугольника, содержащего заданную точку.
Задача поиска многоугольника, содержащего заданную точку, является весьма распространенной в системах, где поверхность моделируется с помощью набора графических примитивов: систем 3D моделирования и проектирования, компьютерных играх и других. Как правило, но не обязательно, таким многоугольником является треугольник. Для того чтобы узнать, к какому многоугольнику относится точка, нужно определить, входит ли точка в данный многоугольник.
Задача принадлежности точки многоугольнику хорошо исследована и имеет множество решений. Некоторые из них являются универсальными и могут применяться к большому количеству типов многоугольников, другие являются специализированными для определенных условий. Чаще всего универсальные алгоритмы сложны в реализации и медленно работают, они применяются тогда, когда нет никакой информации о многоугольнике. В условиях, когда информации достаточно, применяются специализированные алгоритмы [1]. Однако даже самые быстрые алгоритмы принадлежности точки многоугольнику не могут обеспечить приемлимое время работы, если вопрос стоит о сотнях многоугольников. Требуется найти способ, который позволил бы исключить из поиска большую их часть, при этом не зависел бы от типа многоугольника, был простым в реализации и быстрым в работе.
Наиболее часто встречающимся алгоритмом является метод трассировки луча. Из точки проводится луч в произвольном направлении, затем подсчитывается количество пересечений луча и контура многоугольника. Если луч и контур пересекаются нечетное количество раз, то точка находится внутри многоугольника, если четное – снаружи (см. рисунок 1).
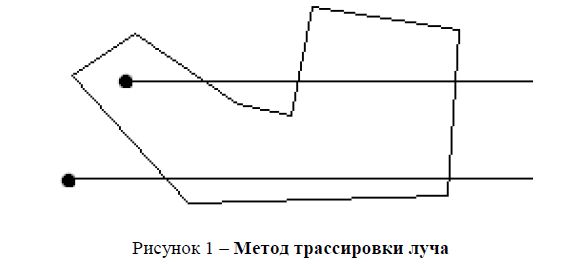
Рисунок 1 – Метод трассировки луча
В общем случае алгоритм подходит как для выпуклых, так и для невыпуклых многоугольников. Однако в некоторых ситуациях он не применим. Например, если луч, выпущенный из точки вне многоугольника, пересечет его вершину, тогда формально пересечение будет одно, что приведет к неправильному результату. Другими подобными случаями будут случаи, когда луч, проведенный из точки, полностью попадает на одно из ребер или точка лежит на ребре. Поэтому для корректного использования этого метода нужно учитывать большое количество исключительных ситуаций, что усложняет реализацию [2].
Другим подходом к решению задачи является тригонометрический алгоритм. Его суть состоит в том, что из точки проводятся лучи ко всем вершинам многоугольника. Для каждой пары вершин вычисляется разность углов лучей, проведенных из точки. Затем разности суммируются. Точка лежит вне многоугольника, если эта сумма равна нулю. Этот алгоритм требует большого количества вычислений обратных тригонометрических функций, поэтому для многоугольников с большим количеством вершин выполняется очень долго [3].
Следующим метод можно описать так: из точки проводятся отрезки ко всем вершинам многоугольника, затем подсчитывается сумма образовавшихся треугольников. Эта сумма в точности совпадает с площадью исходного многоугольника, если точка находится внутри фигуры. Недостаток данного алгоритма в том, что для многоугольника произвольной формы подсчет площади является непростой задачей, заметно усложняющий реализацию. Но в случаях простых многоугольников, например треугольников, этот метод является весьма эффективным [4].
Для сложных многоугольников применяется метод триангуляции, то есть разбиение многоугольника на составляющие его треугольники. Треугольник является весьма удобной фигурой для проверки вхождения в него точки. Проверить, входит ли точка в многоугольник, можно узнав, входит ли точка в хотя бы один из получившихся треугольников. Однако триангуляция не является простой задачей, поэтому к такому методу прибегают лишь в случаях, когда многоугольник слишком сложный для других алгоритмов [5].
Для выпуклого многоугольника существует еще один весьма эффективный алгоритм. Он основан на сравнении положения точки относительно ребер фигуры. В выпуклом многоугольнике любая точка, находящаяся внутри, будет находиться с одной стороны от каждого ребра. Слева или справа - зависит от обхода движения (по часовой стрелке или против).
Определить положение точки относительно ребра, можно, проведя прямую через вершины ребра.
По координатам этих вершин можно вывести уравнение прямой.
Уравнение прямой через две заданные точки:
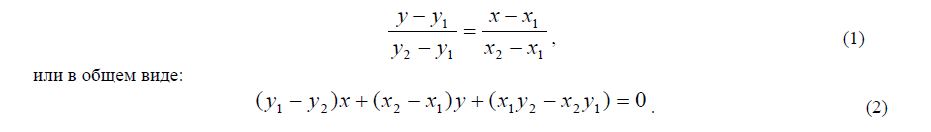
Координаты точки подставляются в данное уравнение. Если результат равен нулю, то точка лежит на прямой (не обязательно на отрезке образованном вершинами ребра). Если число положительное, точка находится слева от прямой, если отрицательное - справа.
Перебрав подобным образом все ребра многоугольника, можно определить, находится ли точка внутри контура или нет [1].
Определившись со способом решения задачи вхождения точки в многоугольник, можно перейти к задаче поиска многоугольника содержащего заданную точку. Ведь перебор всех многоугольников на возможность вхождения в них точки может быть очень долгим процессом. Поэтому имеет смысл исключить из поиска многоугольники, в которые точка заведомо не входит. Наиболее простым и весьма эффективным методом решения этой проблемы является проверка вхождения точки в ограничивающий прямоугольник многоугольника (см. рисунок 2).
Хотя для ограничивающего прямоугольника могут быть применимы вышеперечисленные методы, более быстрым способом является простая проверка координат точки и максимальных координат вершин многоугольника. Очевидно, что если точка располагается левее, чем самая левая вершина многоугольника, то она в него не входит.
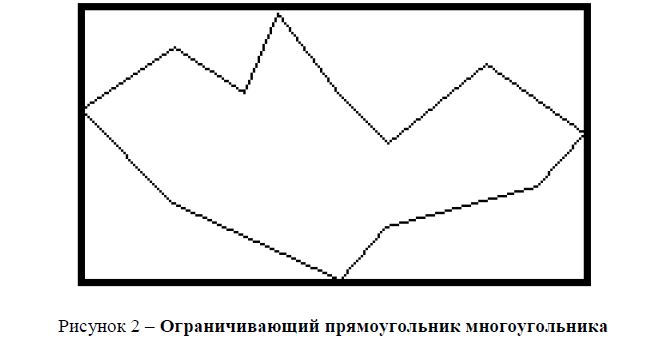
Рисунок 2 – Ограничивающий прямоугольник многоугольника
Обобщая вышенаписанное, можно составить алгоритм поиска многоугольника. Шаг 1: Составить список всех многоугольников.
Шаги 2, 3, 4: Исключить из списка все многоугольники, располагающиеся с одной стороны от точки. Затем со второй, с третьей, с четвертой.
Шаг 5: К оставшимся в списке многоугольникам применить один из алгоритмов определения вхождения точки в многоугольник.
Выигрыш от данного подхода будет тем больше, чем больше количество многоугольников и чем больше вершин они содержат, чем сложнее их форма. Ведь поиск максимальной координаты требует линейного времени O(N) и простых операций сравнения [6].
Таким образом, используя этот метод в комбинации с одним из алгоритмов определения вхождения точки в многоугольник, можно весьма эффективно решать задачу поиска многоугольника, содержащего заданную точку.
Литература
- Препарата Ф., Шеймос М. Вычислительная геометрия: Введение. – М.: Мир, 1989. – 478 с.
- Ласло М. Вычислительная геометрия и компьютерная графика на C++. – М.: БИНОМ, 1997. – 304 с.
- Шикин Е.В. Компьютерная графика. Полигональные модели. – М.: ДИАЛОГ – МИФИ, 2005. –223 с.
- Шикин Е.В. Начала компьютерной графики. – М.: ДИАЛОГ – МИФИ, 2000. – 374 с.
- Скворцов А.В. Алгоритмы построения и анализа триангуляции. – Т.: Издательство Томского университета, 2006. – 167 с.
- Седжвик Р. Фундаментальные алгоритмы на С++. – К.: ДиаСофт, 2001. – 688 с.